Physics-guided Neural Networks (PGNN) : An Application in Lake Temperature Modeling

오늘 다뤄볼 논문은 전반적인 Data Sience와 관련된
'Physics-guided Neural Networks (PGNN) : An Application in Lake Temperature Modeling'라는 논문입니다.
Introduction
우리도 잘 알고 있다시피 빅데이터가 사용되고 있는 요즘,
Data Science는 지식 발견을 위한 필수적 도구로 자리 잡았습니다.
특히 Deep Learning과 같은 Data Science의 발전은
많은 산업분야의 기술을 혁신적으로 발전시켰는데요,
이러한 발전을 고려해 현재 Data Science를 활용한 과학적 지식 발견이 가속화되고 있는 추세입니다.
Related Works
1. Data Science Models

과학적 지식 발견에 사용되는 Data Science Model들은 위 그림에서도 나타나있듯이
오직 데이터에만 의존하여 패턴을 학습하는 것으로 물리적인 원리나 지식은 고려하지 않는 모델입니다.
[한계]
따라서 해당 모델은 데이터를 기반으로 복잡한 관계를 모델링할 수 있다는 장점이 있지만
내부 작동 원리를 설명하기 어렵다는 Black-box와 같은 한계점이 존재합니다.
특히 과학적 도메인 지식을 고려하지 않기 때문에
모델이 알려진 물리법칙과 일치하지 않는다는 문제점이 발생하기도 합니다.
그렇기 때문에 아무리 Data Science Model들이 정확한 성능을 달성한다 하더라도
물리적인 과정을 설명하거나 해석하는 능력이 없으므로 과학적 발견에 사용되기에는 무리가 있음을 언급하고 있습니다.
2. Physics-based Models

과학적 지식 발견에 이용되는 두번째 모델은 Physics-based Model입니다.
마찬가지로 위 그림에서도 볼 수 있다시피
물리학적 원리와 방정식을 기반으로 입출력 간의 관계를 학습하는 모델입니다.
[한계]
앞선 Data Science Model에 비해 물리적 해석 가능성 측면에서 가치가 있는 모델이지만
데이터로부터 지식을 직접 추출하는 능력이 제한적입니다.
또한, 물리학적 모델을 구축하려면 충분한 데이터가 필요한데,
해당 모델은 데이터를 그만큼 사용하지 않기 때문에 모델의 예측 능력이 떨어진다는 문제점이 있습니다.
마지막으로 오로지 물리 원리만 가지고 학습을 하므로 실제 물리과정의 복잡성을 완벽하게 반영하기 어려워
주로 사용 가능한 물리학에만 의존한다는 한계가 존재합니다.
Proposed Method
PGNN(Physics-guided Neural Networks)
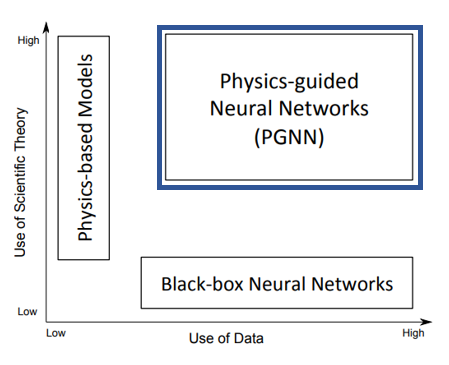
앞선 Data Science Model과 Physics-based Model의 한계를 해결하기 위해
Data Science Model처럼 충분히 데이터를 사용함으로써 예측 능력을 보장하고,
Physics-based Model 처럼 물리적 원리를 반영함으로써 물리적 해석이 가능한 모델을 제안하고자 하였습니다.
이에 Physics-based Model과 Nerual Network를 결합한 Physics-guided Nerual Networks(PGNN)이라는
모델을 제안하였고, PGNN은 총 2가지 단계를 걸쳐 학습이 진행된다는 특징이 있습니다.
Step 1. Constructing Hybrid-Physics-Data (HPD) Models
첫 번째 단계는 Hybrid-Physics-Data(HPD) Models를 구축하는 것입니다.
이 단계를 이해하기 위해 실제 관측 값인 Y와 입력 데이터인 D가 있다고 가정해 보겠습니다.
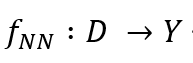
이러한 가정 속에서 fNN(Data Science Model)은
관측 데이터를 기반으로 Y의 예측 값을 생성하게 됩니다.
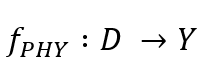
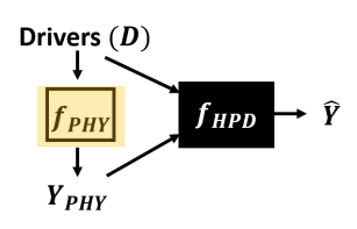
반면, fPHY(Physics-based Model)는 입력 데이터인 D와의 물리적 관계를 기반으로
시뮬레이션을 하여 출력 값인 YPHY를 생성하게 됩니다.
[fPHY(Physics-baed Mdoel)의 한계]
하지만 fPHY(Physics-based Model)의 경우 데이터를 사용하여 모델 파라미터를 보정해야 하는 작업이 필요한데,
이는 많은 시간이 소요된다는 문제점이 있습니다.
또한 모델에 물리학적 내용이 부족할 경우,
출력 값인 YPHY와 실제 관측 값 Y 사이에 불일치가 발생하게 됩니다.
[Sol]
이에 본 논문은 fPHY(Pysics-based Model)와 fNN(Data Science Model)을 결합하여
물리적 관계와 관측 데이터를 모두 활용하는 Hybrid-Physics-data (HPD) Model을 제안하였습니다.

fPHY(Pysics-based Model)와 fNN(Data Science Model)을 결합하는 방법은
그림에서도 알 수 있다시피 fPHY(Pysics-based Model)의 출력 YPHY를 입력데이터인 D와 함께
fNN(Data Science Model)의 또 다른 입력으로 활용하는 것입니다.
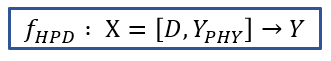
해당 내용을 수식으로 표현하자면 위와 같습니다.
만약 fPHY(Pysics-based Model)가 정확하여 출력 값인 YPHY와 실제 관측 값 Y가 완벽하게 일치한다면 좋겠지만,
YPHY에 불일치 및 편향이 존재할 수도 있기 때문에 Hybrid-Physics-data (HPD) Model은 이를 해결하기 위해
입력 데이터 공간으로부터 특징을 추출함으로써 불일치를 줄이고자 하였습니다.
그렇게 본 논문에서는 Hybrid-Physics-data (HPD) Model에 물리학적 손실함수를 도입하였고,
이를 통해 모델이 물리적 원리를 보다 잘 학습하도록 하였습니다.
Step 2. Using Physics-based Loss Functions
그렇게 두 번째 단계는 물리학적 손실함수를 사용하는 것입니다.
이 단계를 더 잘 이해하고자 일반적인 모델의 학습 목표, 즉 손실함수에 대해 알아보겠습니다.
* 일반적인 모델의 학습 목표
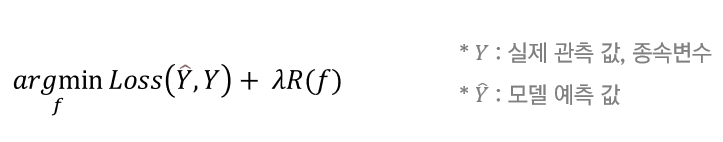
첫 번째 항은 모델의 예측 값과 실제 값 간의 차이를 의미하며
모델의 예측 값이 실제 값과 가장 유사하도록 이를 최소화하는 방향으로 학습하게 됩니다.
두 번째 항에 포함된 R(f)는 모델의 복잡성을 나타내는 함수로서
모델이 복잡하면 함수 값이 증가하고 단순하면 감소하기 때문에 과적합을 방지하기 위해 최소화시키고자 하였습니다.
또한, 두 번째 항에 포함된 람다는 모델의 복잡성을 조절하는 하이퍼파라미터로
과적합을 방지함과 동시에 새로운 데이터에 대해서도 좋은 일반화 능력을 유지할 수 있게끔 사용되었습니다.
[Prob]
이처럼 일반적인 모델은 위 식과 같은 손실함수를 최소화하는 방향으로 학습하는데,
이는 물리학적 지식과 일치하지 않는 결과를 생성한다는 문제가 있습니다.
1. 물리학적 제약식 정의

이를 해결하기 위해 본 논문은 물리학적 원리를 포함한 손실함수를 만들고자
가장 먼저 물리학적 제약식을 정의하였습니다.
첫 번째 방정식은 Y와 Z 사이의 물리학적 관계가 0이 되어야 함을 의미하는 관계식으로
예시로는 뉴턴의 운동 법칙과 같은 방정식이 이에 포함됩니다.
두 번째 방정식은 Y와 Z 사이의 물리학적 관계가 0 이하의 값을 가져야 함을 의미하는 관계식으로
예시로는 유체의 속도와 압력 간의 관계가 있습니다.
이렇게 물리적인 상황에서 변수들 간의 관계를 설명하는 물리학적 제약을 정의함으로써
모델이 예측할 때 위와 같은 물리학적 법칙을 따르게끔 하였습니다.
이를 통해 모델은 물리학적 지식을 포함하면서도 데이터로부터 효과적인 학습 및 예측이 되도록 하여
물리학적 일관성과 신뢰성까지 보장하게 됩니다.
2. 물리학적 손실함수 정의
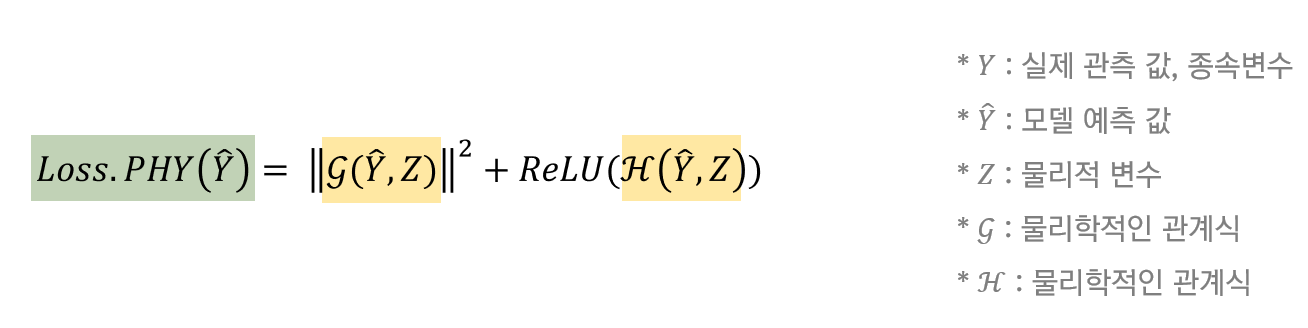
위와 같이 정의한 물리학적 제약식을 활용하여 물리학적 손실함수를 수립하였고,
PGNN은 이러한 손실함수를 포함하여 학습하게 됩니다.
쉽게 말해 위 수식은 모델이 앞서 정의한 물리학적 제약식을 얼마나 따르는지 측정하기 위해 도입되었습니다.
첫 번째 항의 경우, 첫번째 방정식의 위반 정도를 측정합니다.
모델의 예측 값과 물리학적 관계 사이의 차이를 제곱함으로써
0에 가까울수록 일관성이 있고 값이 클수록 위반했다고 판단하도록 하였습니다.
두 번째 항은 앞서 보여드린 두번째 방정식의 위반 정도를 측정합니다.
이 항에는 ReLU 함수를 적용하였는데,
ReLU 함수는 입력 값이 0보다 작으면 0으로 만들고 0보다 크면 입력 값을 그대로 반환하는 특징이 있습니다.
따라서 이러한 ReLU 함수를 통해 0보다 큰 값만 고려함으로써
이 값이 작을수록 모델 예측이 물리학적으로 일관성 있음을 나타내고자 하였습니다.
3. 물리학 기반 모델(PGNN)의 학습 목표 수립
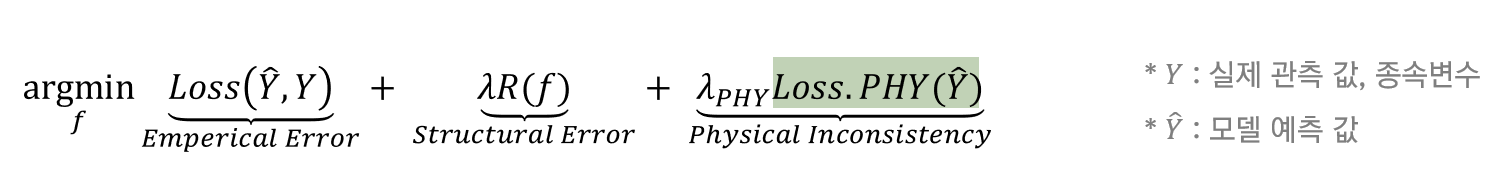
그렇게 수립한 물리학적 손실함수 Loss.PHY를 PGNN의 학습 목표에 추가시켰습니다.
첫 번째 항과 두 번째 항은 처음 보여드린 일반적인 모델의 학습 목표와 동일합니다.
세 번째 항은 일반적인 모델의 학습 목표에서 추가된 항인데,
이 항은 모델의 예측이 물리학적 관계를 얼마나 잘 따르는지를 측정하는 항으로 사용되었으므로
이를 최소화하는 방향으로 학습하고자 하였습니다.
특히 Loss.PHY에 곱해진 하이퍼파라미터 람다 PHY는
모델이 물리학적 제약을 얼마나 엄격하게 따를지 조절하는 용도로 활용되었습니다.
즉, 하이퍼파라미터 람다 PHY가 크면 모델이 물리학적 제약을 엄격하게 따르도록 함을 의미하며
결과적으로 모델이 물리학적으로 더 일관된 예측을 하게 됩니다.
반대로 값이 작으면 모델이 물리학적 제약을 덜 따라도 됨을 의미함으로써
모델에게 더 자유롭게 데이터를 학습하도록 허용하여 물리학적 일관성을 강제하지 않습니다.
결국, 해당 하이퍼파라미터의 크기는 모델이 데이터와 물리학적 지식 사이의 균형을
어떻게 맞출지 결정하는 용도로 사용되었습니다.
* 확률적 경사하강법 (SGD) 최적화 알고리즘 사용
결론적으로 PGNN은 일반적인 모델의 학습 목표와 달리 Empricial Error, Structural Error 외에도
Physical Inconsistency라는 항까지 최소화시키는 방향으로 학습하였습니다.
이를 통해 PGNN은 물리적 일관성을 유지하면서도 실제 데이터와 일치하는 정확도를 보이며
모델의 복잡성까지 적절히 제어 가능하다는 장점을 가지고 있습니다.
본 논문에서는 이러한 PGNN의 효과를 보고자 호수 온도 모델링 문제에 적용하였습니다.
Physics-guided Neural Networks (PGNN) for Lake Temperature Modeling
본 논문이 다양한 물리적 문제들 중,
호수 온도 모델링 문제에 PGNN을 적용시키게 된 배경에 대해 알아보겠습니다.
호수의 물 온도는 물고기의 성장, 생존 및 번식을 제어하기 때문에
생태계에 큰 영향을 미치는 중요한 요소입니다.
특히 물 온도의 상승은 외래 어류의 침입과 해조류 번식 증가와 관련이 있기 때문에
정확한 호수 온도 모델링이 필요합니다.
[Prob]
하지만 호수의 공간 규모가 큰 경우,
물 온도 관측 데이터가 부족하거나 없을 수도 있습니다.
또한, 호수 물 온도 모델링에 있어서는 깊이와 시간을 고려해야 한다는 점이 중요한데
이렇게 복잡한 물리적 과정을 정확히 모델링하려면 다양한 파라미터가 필요합니다.

이러한 문제점을 해결하기 위해 다양한 물리 기반 모델들이 개발되었는데,
그중 본 논문은 General Lake Model(GLM)을 언급함으로써 제안한 PGNN과 비교하고자 하였습니다.
General Lake Model(GLM)은 물 온도 변화에 영향을 미치는
다양한 물리적 요소 및 파라미터를 포함합니다.
ex) 태양 복사에 의한 물의 가열, 다양한 깊이에서의 에너지 혼합, 표면에서의 열 방출 등
[Prob]
하지만 각 호수마다 General Lake Model(GLM)의 파라미터 값을 사용하기 위해서는
해당 호수에 대한 관측 데이터가 충분히 필요합니다.
또한, 본 모델을 사용하여 모델의 정확도를 높이기 위해서는 각 호수에 대한 세부적인 맞춤 작업이 필요한데,
이러한 작업은 파라미터의 모든 가능한 조합에 대해 모델을 실행해야 하고
실제 값과 비교하기 위해 많은 노력과 시간이 필요하므로 한정된 수의 호수에서만 수행할 수 있습니다.
즉 , General Lake Model(GLM)에는 모델 정확도 향상과 연구 범위 확장 간에
trade-off 관계가 존재한다는 한계가 있습니다.
[Sol]

따라서 더 다양한 호수에 대해 정확한 모델링을 하고자
PGNN 모델을 호수 온도 모델링 문제에 적용하게 되었습니다.
앞서 설명드린 PGNN의 프레임워크를 따르면
첫 번째 단계였던 Hybrid-Physics-data (HPD) Model을 구축하기 위해
fPHY(Pysics-based Model)로 General Lake Model(GLM)를 사용하였으며,
General Lake Model(GLM)의 출력인 YPHY와 입력 데이터 D를 결합하여 새로운 입력 X를 생성하였습니다.
그리고 PGNN의 핵심 아이디어인 물리학적 지식을 신경망 학습에 사용하기 위해
호수 온도 모델링 문제에서는 물의 온도, 밀도 및 깊이 사이의 중요한 물리적 관계를 손실함수에 포함시켰습니다.
(1) Temperature-Density Relationship
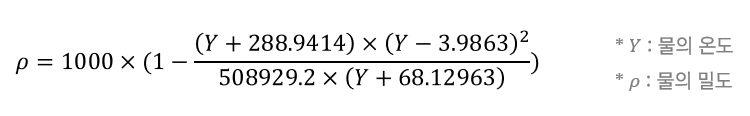
첫번째 물리적 관계는 온도와 밀도 사이의 비선형 관계를 나타내는 물리적 제약식입니다.
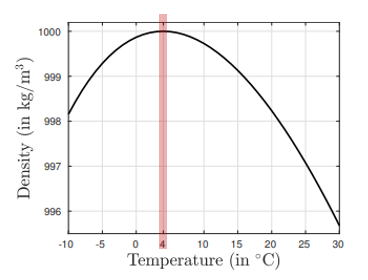
위 그림은 수식에서 표현된 물리적 관계를 시각적으로 나타낸 것으로 물은 4도에서 가장 밀도가 높다는 것을 볼 수 있고,
모델은 이러한 물리학적 이론을 첫번째 방정식을 통해 학습하게 됩니다.
(2) Density-Depth Relationship

두 번째는 물의 밀도와 깊이 간의 관계를 나타내는 물리적 제약식입니다.
수식을 조금 더 자세히 살펴보자면 같은 시간 t에서 다른 깊이 수준인 d1과 d2의 물의 밀도를 비교했을 때,
d1이 d2 보다 얕은 경우 밀도 차이는 0보다 작거나 같아야 함을 나타냅니다.
즉, 얕은 깊이의 물의 밀도가 더 낮아야 한다는 물리적 관계를 의미합니다.
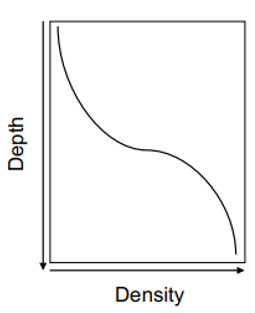
그렇게 위 그림은 두 번째 물리적 관계를 시각적으로 나타낸 것으로
밀도가 높은 물은 더 무겁기 때문에 물이 깊어짐에 따라 밀도가 단조 증가하고 있음을 보여주고 있고
마찬가지로 PGNN 모델은 이러한 물리학적 원리를 두번째 방정식을 통해 학습하게 됩니다.
(3) Physics-based Loss Function

위 수식은 특정 깊이 di에서 예측된 밀도와
그다음 깊이 di+1에서의 예측된 밀도 간의 차이를 나타내는 수식인데,
깊이가 깊어질수록 물의 밀도는 증가한다는 물리학적 원리에 따라
di+1의 깊이가 di보다 깊기 때문에 위 수식은 0 또는 음의 값을 가져야 합니다.
따라서 위 수식은 모델이 물리학적 법칙을 위반한 정도를 측정하는 데에 사용되고,
이는 PGNN의 손실함수에 포함되어 모델이 호수 물 온도와 관련된 물리학적 원리를 학습하게끔 합니다.
(4) 호수 온도 모델링 문제에서의 학습 목표

그렇게 앞서 보여드렸던 수식은 PGNN의 손실함수에 포함되게 되고,
위 수식은 물리학적 관계 위반을 종합적으로 측정하게 됩니다.
그리고 ReLU 함수를 사용함으로써 물리학적 관계를 위반한 경우만 고려하게 되므로
이 값이 낮을수록 모델의 예측이 물리적 관계와 더 일치함을 나타냅니다.
이렇게 PGNN은 물리학적 손실함수를 사용하여 학습함으로써
더 정확한 온도 예측과 함께 밀도 및 깊이와 같은 물리학적 변수 간의 일관성을 보장하게 됩니다.
Experiment
Data
실험에는 크기가 상당히 큰 미네소타주의 밀 락 호수와 위스콘시주의 맨도타 호수 온도 데이터가 활용되었습니다.
특히 두 호수는 다른 호수들에 비해 충분한 관측 기록을 가지고 있고,
깊이에 따른 온도 변화가 시간에 따라 다양하게 나타났기 때문에 실험에 사용되었다고 말하고 있습니다.
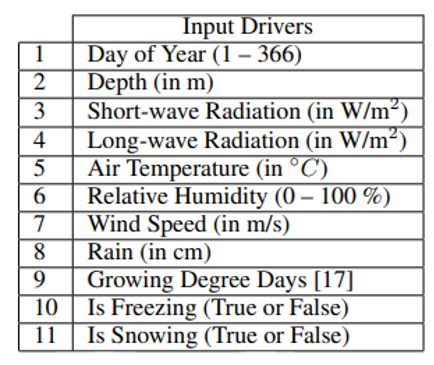
또한, 각 관측치마다 위 표에 나타난 11개의 기상변수가 입력 변수에 사용되었고
각 호수에 대한 정확한 데이터는 아래와 같습니다.
* Mille Lacs Lake : 1981년 6월 17일 ~ 2016년 1월 1일, 총 7072개의 온도 관측치
* Mendota Lake : 1980년 4월 30일 ~ 2015년 11월 2일, 총 13543개의 온도 관측치
실험에서는 호수 온도 모델링에 fPHY(Pysics-based Model)로 General Lake Model(GLM)를 사용하였으며,
모델의 일반화 성능을 평가하기 위해 관측된 온도 데이터 외에도 관측되지 않은 가상 데이터를 생성함으로써
General Lake Model(GLM)의 출력인 YPHY 값을 생성하였습니다.
Baseline Methods
본 논문에서는 PGNN 모델의 성능을 평가하기 위해 총 3가지 모델과 함께 비교하고자 하였습니다.
(1) PHY (Physics-based Models)
먼저, 물리학 기반 모델인 PHY로는 General Lake Model(GLM)가 사용되었으며
이는 데이터보다는 물리학적 원리를 위주로 학습된 모델입니다.
(2) Black-box Models (Data Science Models)
두 번째는 Black-box라는 한계점을 가진 Data Science Model로
여기에는 세 가지 표준 비선형 모델인 SVM, LSBoost, 신경망(NN) 모델이 사용되었는데,
위 모델들은 PGNN과 동일한 입력 데이터를 사용하여 호수의 온도를 예측하지만
물리학적 지식이 포함된 손실함수는 사용하지 않습니다.
(3) PGNN0
앞서 살펴봤다시피 PGNN은 총 2가지의 단계를 거치는데,
PGNN0는 오로지 step 1, 즉 Data Science Model과 Physics-based Model을 결합한 하이브리드 방식으로만 작동될 뿐
PGNN처럼 물리학 기반 손실함수를 사용하지는 않아 물리학적 일관성을 강조하진 않는 모델입니다.
Evaluation Metrics
그리고 본 실험에서는 2가지 평가지표를 사용하였습니다.
(1) RMSE(Root Mean Squared Error)
이는 모델이 테스트 데이터에서 얼마나 정확한 예측을 하는지를 나타내는 지표로
값이 낮을수록 예측이 실제 관측과 가깝다는 것을 의미합니다.
(2) Physical Inconsistency
PGNN의 주요 기여 중 하나가 물리적으로 일관된 예측을 보장하는 것인데,
이는 모델이 얼마나 물리학적으로 일관되지 않은 예측을 하는지 측정하는 지표입니다.
즉, 값이 클수록 모델이 물리학적 관계를 반영하지 못한다는 것을 의미함으로써
앞서 살펴봤던 아래의 수식을 통해 물의 밀도-깊이 관계가 위배되는 경우를 파악하고자 하였습니다.

1. Performance Comparison
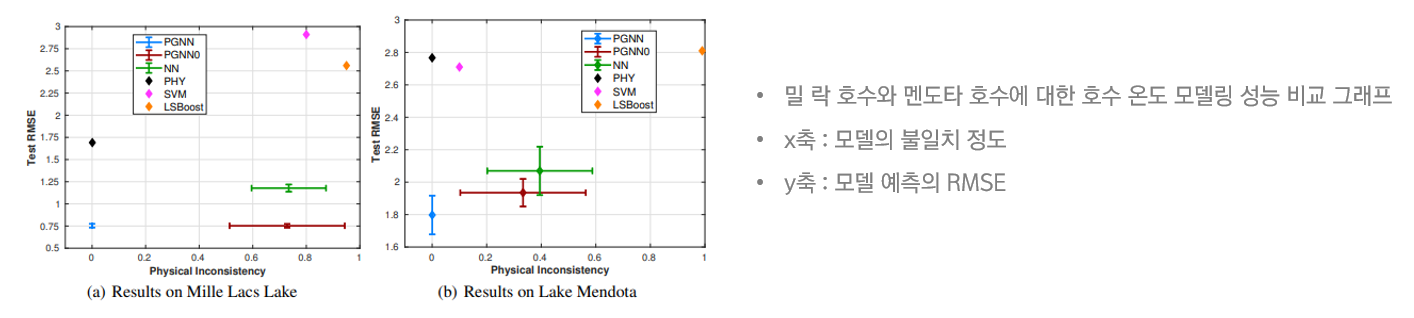
첫 번째로 진행된 실험은 앞서 보여드린 세 가지 모델들과 PGNN을 비교한 실험입니다.
해당 실험을 통해 위와 같은 호수 온도 모델링 성능 비교 그래프가 도출되었는데,
각 점의 수직 방향은 모델의 평균 RMSE를 나타내며, 수평 방향의 위치는 모델의 Physical Inconsistency를 나타냅니다.
그림 (a)
NN은 물리학 지식을 사용하지 않았기 때문에
PHY보다 더 높은 Physical Inconsistency 값을 가지는 것을 볼 수 있습니다.
PGNN0의 경우, 하이브리드 모델을 사용함으로써 NN 보다는 낮은 RMSE 값을 가지지만
물리적 일관성에서는 NN과 차이가 없음을 보입니다.
반면, PGNN은 다른 모델들과 달리 물리학 기반 손실함수를 사용하였기 때문에
가장 낮은 RMSE와 Physical Inconsistency 값을 달성했음을 볼 수 있습니다.
그림 (b)
무엇보다 맨도타 호수가 밀 락 호수보다 온도 역학이 복잡해서 모델링이 어려웠음에도
PGNN은 다른 모델들과 달리 물리적으로 일관성을 유지하면서도 낮은 RMSE 값을 달성하였습니다.
2. Effect of Varying Training Size
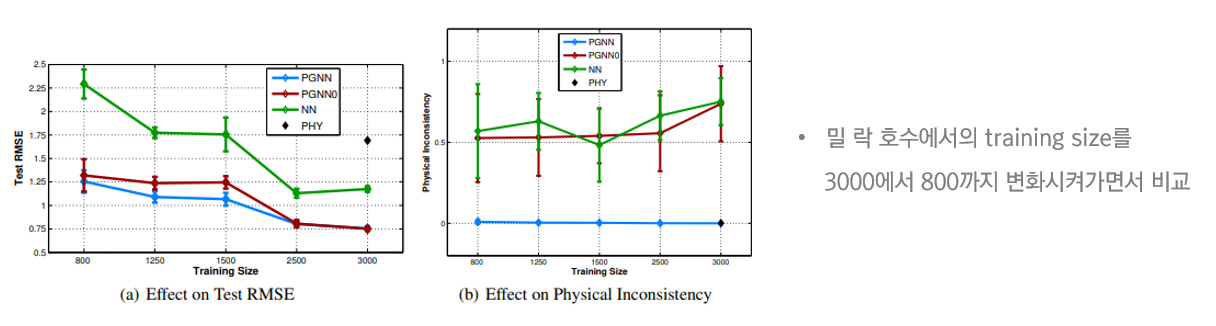
두 번째는 모델을 학습시키는 데 사용되는 training size가
모델 성능에 어떠한 영향을 미치는지 알아보기 위해 진행된 실험으로
밀 락 호수에서의 training size를 3000에서 800까지 변화시켜 가면서 비교해 보았습니다.
다른 모델들은 training size를 줄이면 RMSE와 Physcial Inconsistency 값이 급격히 증가하게 되는데
PGNN0와 PGNN은 점진적으로 증가하고 있는 결과를 통해
PGNN은 데이터의 크기가 작아도 다른 모델들에 비해 우수한 성능을 제공함을 알 수 있습니다.
3. Sensitivity to hyperparameter

세 번째로는 PGNN의 손실함수에 포함되어 있었던 하이퍼파라미터인 람다 PHY 값을 변화시켜 가면서
모델의 성능에 어떠한 영향을 미치는지 실험하였습니다.
(a) Effect on Physcial Inconsistency
Physical Inconsistency의 경우, 높은 하이퍼파라미터 값을 설정할수록 더 강한 물리학적 제약이 가해지기 때문에
물리적으로 일관된 예측을 생성하고 있음을 볼 수 있습니다.
(b) Effet on Test RMSE
반면, 모델의 예측 성능에는 하이퍼파라미터의 변화가 큰 영향을 미치지 않는 것을 확인할 수 있습니다.
이는 모델에 물리학 기반의 손실함수를 이미 도입하였기 때문에
모델이 물리학적 제약을 하이퍼파라미터 없이도 충분히 학습했기 때문입니다.
즉, 모델은 물리학 기반 손실함수를 사용함으로써 물리적으로 일관된 예측을 생성하면서도
예측 성능을 크게 저하시키지 않음을 본 실험을 통해 알 수 있었습니다.
Analysis of Results
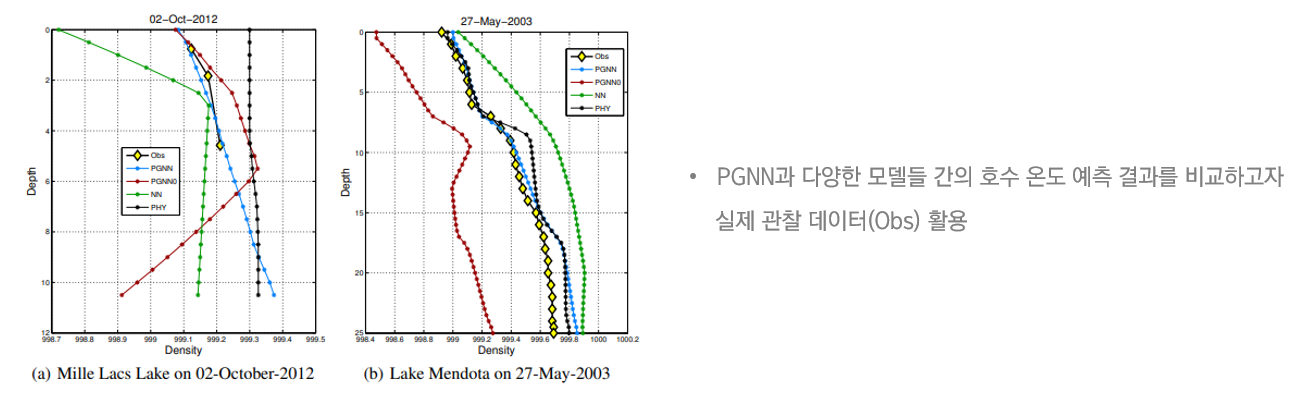
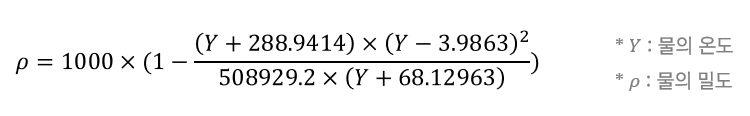
마지막으로 진행된 실험은 위 수식을 통한 PGNN과 다양한 모델들 간의 호수 온도 예측 결과를 비교하는 실험으로
그림에서 노란색 다이아몬드로 표현되어 있는 실제 관찰 데이터(Obs)를 활용하였습니다.
물리학 기반 모델인 PHY의 밀도 추정 값은 실제 관찰 데이터와 다소 차이가 있지만
PGNN은 가장 일치하는 값을 생성함을 볼 수 있습니다.
특히 PGNN의 중간 단계인 PGNN0의 경우, 깊이가 증가함에 따라 밀도가 증가해야 하는데
물리적으로 모순된 결과를 나타냄으로써 본 논문은 물리학 기반 손실함수 활용의 이점을 강조하고 있습니다.
Conclusion
다시 정리하자면, 본 논문이 제안한 PGNN은
Data Science Model과 Physics-based Model의 한계를 해결하고자 한 하이브리드 모델입니다
이를 위해 물리학 기반 모델의 출력을 활용하고, 물리학 기반 손실함수를 사용하여
신경망을 학습시킴으로써 물리적으로 일관된 결과를 보였습니다.
무엇보다 실험을 통해서도 보았다시피 적은 데이터셋과 복잡한 물리학적 모델링이 필요한 순간에서도
높은 예측 성능과 물리적으로 일관된 결과를 보인다는 것이 PGNN의 강점이라고 생각됩니다.
또한, 본 논문의 Contribution은 제약식을 Loss Function에 추가함으로써 최적화 기반으로
보다 더 나은 성능을 제공하고자 함이 아닐까 싶습니다.
하지만 과연 모델이 수립한 제약식에 완벽히 일치할 수 있을까에 대한 고민이 들었던 논문이었습니다.
