| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- deeplearning
- 지도학습
- RegressionTree
- 시계열 데이터
- 데이터분석
- 분류
- 잔차분석
- 비지도학습
- 다중선형회귀분석
- 단순선형회귀분석
- DataScience
- time series
- 결정계수
- 선형회귀분석
- Python
- LinearRegression
- 손실함수
- dataframe
- 로지스틱회귀분석
- 하이퍼파라미터
- machinelearning
- 의사결정나무
- scikitlearn
- 딥러닝
- ML
- OrdinalEncoder
- GridSearchCV
- LogisticRegression
- 데이터전처리
- 시계열데이터
- Today
- Total
IE가 어른이 되기까지
[Machine Learning] 다중 선형 회귀분석에서의 변수 선택 (다중공선성 해결방법) 본문

https://piscesue0317.tistory.com/37
[Data Science] 다중공선성이란 무엇일까요 ?
https://piscesue0317.tistory.com/36 [Machine Learning] 다중 선형 회귀분석 ( 지도학습 / 예측 ) https://piscesue0317.tistory.com/34 [Machine Learning] 선형 회귀분석 ( 지도학습 / 예측 ) https://piscesue0317.tistory.com/27 [Data Scien
piscesue0317.tistory.com
위 글을 통해 다중 선형 회귀분석에서 발생할 수 있는
다중공선성에 대해 알아보았습니다.
이번엔 다중공선성을 해결할 수 있는 방법에 대해 알아보겠습니다.
일단 크게 변수를 줄이거나 추가하는 방법과
줄이지 않는 방법으로 나눌 수 있습니다.
변수를 줄이거나 추가하는 방법 (변수 선택)
변수 선택은
변수가 여러 개일 때 최적의 변수 조합을
찾아내는 기법입니다.
1. All Possible Regressions
변수의 수가 p개일 때 변수의 총조합은 2의 p제곱으로
변수의 수가 증가함에 따라 변수 조합의 수도
기하급수적으로 증가합니다.
이들에 대한 모든 회귀분석을 수행한 후
적절한 기준 (MSE, R square 등) 에 의해 회귀모형을 선택합니다.
| SSEp | Cp | R square | Adj R square |
| 작을수록 좋음 | p + 1에 가까운 모형 중 작을수록 좋음 |
클수록 좋음 | 클수록 좋음 |
* SSE = p개의 회귀계수를 포함한 회귀모형의 잔차제곱합
(모든 k개의 회귀변수가 모형에 포함되었을 때의 MSE값 사용)

2. Forward Selection 방법
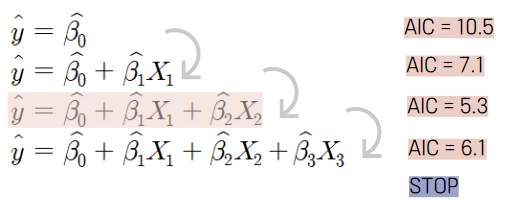
R square 증가에 가장 크게 기여하는 변수부터 하나씩 추가해 가며
성능지표를 비교해가는 방법입니다.
즉, 더 이상 통계적으로 기여도가 유의하지 않다고
판단될 때의 모형을 선택합니다.
AIC : 주어진 데이터 셋에 대한 통계 모델의 상대적인 품질을 평가하는 것 (낮을수록 좋음)
* - 2ln(L) : 모형의 적합도를 의미
* L : Likelihood function
* k : 모형의 추정된 파라미터의 개수
= 따라서 AIC값이 낮다는 것은 모형의 적합도가 높다는 것을 의미
3. Backward Elimination

모든 회귀변수가 포함된 모형에서
통계적으로 유의하지 않은 변수를 하나씩 제거해 나가면서
더 이상 제거할 회귀변수가 없다고 판단될 때의 모형을 선택합니다.
4. Stepwise Regression
회귀변수의 추가와 제거를 병행해 나가되
더 이상 추가할 변수나 제거할 변수가 없을 때까지
계속하는 방법입니다.
변수를 줄이지 않는 방법
* Auto Encoder 등의 Feature Extraction 기법 (딥러닝)
* PCA (주성분 분석)
* Ridge
'ML > Algorithms' 카테고리의 다른 글
| [Machine Learning] 의사결정나무 (지도학습 / 분류) (0) | 2023.01.12 |
|---|---|
| [Machine Learning] 의사결정나무 (지도학습 / 예측) (0) | 2023.01.12 |
| [Machine Learning] 다중 선형 회귀분석 ( 지도학습 / 예측 ) (0) | 2023.01.09 |
| [Machine Learning] 단순 선형 회귀분석 ( 지도학습 / 예측 ) (0) | 2023.01.09 |
| [Machine Learning] 선형 회귀분석 ( 지도학습 / 예측 ) (0) | 2023.01.06 |





