| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 선형회귀분석
- scikitlearn
- machinelearning
- 딥러닝
- 지도학습
- 다중선형회귀분석
- DataScience
- dataframe
- Python
- time series
- 의사결정나무
- 분류
- 시계열 데이터
- GridSearchCV
- 단순선형회귀분석
- LinearRegression
- deeplearning
- RegressionTree
- 데이터전처리
- LogisticRegression
- ML
- 비지도학습
- 로지스틱회귀분석
- 결정계수
- OrdinalEncoder
- 손실함수
- 하이퍼파라미터
- 시계열데이터
- 잔차분석
- 데이터분석
- Today
- Total
IE가 어른이 되기까지
[Time Series] 시계열 데이터 처리 및 EDA : 요소 분해 본문

https://piscesue0317.tistory.com/75
[Time Series] 시계열 데이터란 ?
이번 글에서는 시계열 데이터가 무엇이고어떠한 특징을 가지고 있는지 알아보겠습니다. 1. 시계열 데이터 보통 우리가 다루는 비시계열 데이터란 위처럼 한 시점에 여러 변수에 대해
piscesue0317.tistory.com
위 글에서는 시계열 데이터가 무엇인지에 대해 알아보았고
시계열 데이터를 모델에 넣어 분석하기 전, 주요 패턴을 제거해야
신뢰성 있는 예측 결과를 얻을 수 있다는 얘기를 나눠보았습니다.
이번 글부터는 시계열 데이터의 주요 패턴을 제거하는 다양한 전처리 방법에 대해 알아보겠습니다.
| 추세성, 계절성이 존재하는 경우 : 차분 (Differencing) 변동 요인이 고정적인 패턴을 보이지 않는 경우 : 평활화 (Smoothing) 변동 요인이 고정적인 패턴을 보이는 경우 : 요소 분해 (Decomposition) |
앞서 다뤄봤었던 시계열 데이터에서의 변동 요인들이 어떠한 특징을
보이느냐에 따라 적용하는 전처리 방식이 다릅니다.
이번 글에서는 그중에서도 요소분해에 대해 알아보겠습니다.
요소분해

위 그림과 같이 시계열 데이터는 우연변동, 추세변동, 계절변동, 주기변동 등
다양한 변동의 성분이 중첩되어있는 것을 볼 수 있습니다.
이러한 시계열 데이터에서는 추세 및 주기의 유무와 크기를 파악하는 일이 매우 중요한데
시계열 데이터를 우연변동, 추세변동, 주기변동으로 구분하여 분해하는 방법을 요소분해라고 합니다.
요소분해를 통해 중첩된 변동요인을 분해하는 이유는
시계열 데이터에서 추세변동과 주기변동을 제거함으로써 남은 잔차 시계열 데이터를
우연변동에 의한 정상 시계열 데이터로 만들 수 있기 때문입니다.
요소분해는 시계열 데이터를 추세 및 주기변동(TC), 계절변동(S), 우연변동(I)으로 구분하여 성분을 추출하는데
이때 분해방법에 따라 가법모형(Additive)과 승법모형(Multiplicative)로 구분하며
각각 어떠한 방법으로 분해하는지 알아보도록 하겠습니다.
1. 가법 모형

가법 모형은 시계열 데이터가 추세변동, 주기변동, 우연변동의 합으로 이루어진 것으로
간주하기 때문에 이처럼 선형적인 형태로 구성됩니다.

예를 들어 이렇게 계절성만 존재하는 시계열 데이터가 있다고 가정해 보겠습니다.

위와 같은 시계열 데이터를 추세변동, 계절변동, 우연변동으로 분해해 본 결과
추세성은 존재하지 않았기 때문에 추세변동에서는 일정한 패턴이 존재하지 않았고
계절변동은 일정한 패턴을 보이는 것을 알 수 있었으며
우연변동 또한 어떠한 패턴도 존재하지 않았기 때문에 분해를 잘 해냈다고 판단할 수 있습니다.
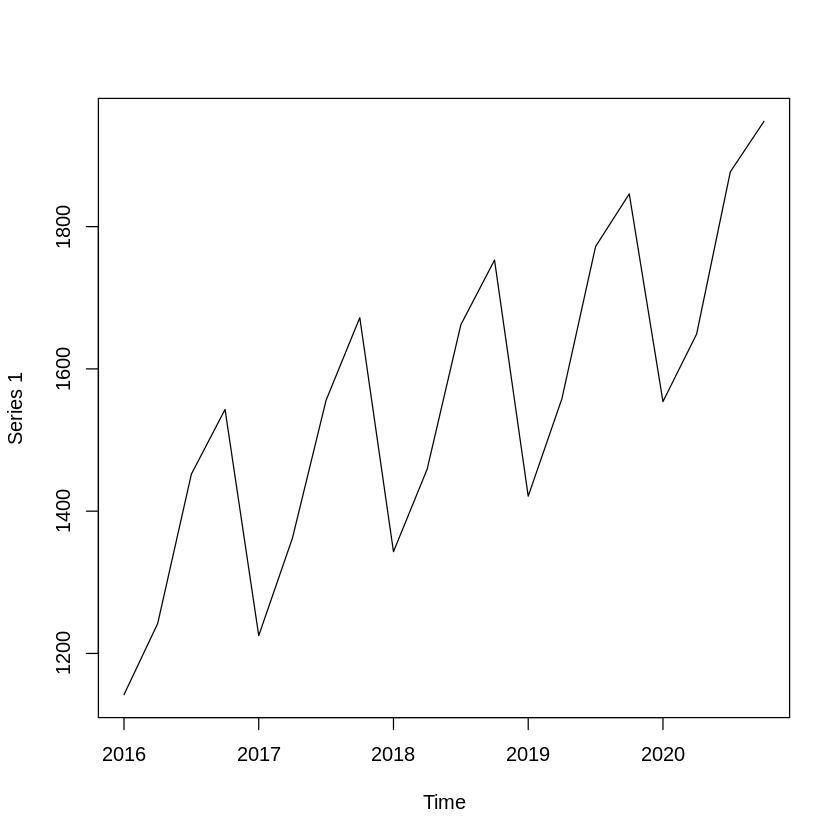
이번에는 계절성과 추세성이 모두 존재하는 시계열 데이터가 있다고 가정해 보겠습니다.

이때 이들을 모두 분해해 본 결과 추세변동과 계절변동 모두 일정한 패턴을 보이는 것을 알 수 있고
우연변동 또한 어떠한 패턴도 존재하지 않았기 때문에 분해를 잘 해냈다고 판단할 수 있습니다.
2. 승법 모형

승법 모형은 시계열 데이터가 추세변동, 주기변동, 우연변동의 곱으로 이루어진 것으로
간주하기 때문에 이처럼 비선형적인 형태로 구성됩니다.
승법 모형에서 Log 변환을 실시하면 곱하기 형태가 더하기 형태로 변하기 때문에
가법 모형의 식으로 변환시킬 수 있습니다.
다만 승법 모형을 사용하려면 데이터에 0이 존재해서는 안되겠지요 ?
만약 0이 존재한다면 그 어떠한 값에도 관계없이 결과가 0이 되기 때문입니다.

이번에는 추세에 따라 변동폭이 증가하는 형태의 시계열 데이터에 대해 다뤄보도록 하겠습니다.


이러한 데이터를 각각 가법모형과 승법모형으로 분해해 본 결과
두 모형 모두 추세변동과 계절변동은 잘 분해해 낸 것을 볼 수 있지만
비교적 가법모형으로 분해된 우연변동에서는 미미한 패턴이 보이는 것을 알 수 있습니다.
위 데이터로 알 수 있는 가법 모형과 승법 모형의 차이점은
가법 모형은 추세변동과 계절변동이 서로 독립적이라고 가정하지만
승법 모형은 추세변동에 따라 계절변동이 변화한다고 볼 수 있는 경우에 이용됩니다.

따라서 왼쪽처럼 시간이 지남에 따라 변동폭이 일정하면 가법모형을 쓰는 것이,
오른쪽처럼 시간이 지남에 따라 변동폭이 증가하는 경우에는 승법모형을 쓰는 것이 적절합니다.
'STUDY > Temporal Data Science' 카테고리의 다른 글
| [Time Series] 시계열 데이터 처리 및 EDA : 평활화 (9) | 2024.09.02 |
|---|---|
| [Time Series] 시계열 데이터 처리 및 EDA : 차분 (0) | 2024.08.30 |
| [Time Series] 시계열 데이터란 ? (2) | 2024.08.28 |



