| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
- 잔차분석
- 다중선형회귀분석
- Python
- ML
- 비지도학습
- 선형회귀분석
- OrdinalEncoder
- 시계열 데이터
- scikitlearn
- time series
- GridSearchCV
- DataScience
- LogisticRegression
- 의사결정나무
- 로지스틱회귀분석
- RegressionTree
- 단순선형회귀분석
- dataframe
- 손실함수
- 결정계수
- 분류
- 하이퍼파라미터
- 시계열데이터
- machinelearning
- LinearRegression
- deeplearning
- 데이터분석
- 지도학습
- 딥러닝
- 데이터전처리
- Today
- Total
IE가 어른이 되기까지
[Machine Learning] 로지스틱 회귀분석 (지도학습 / 분류) 본문

https://piscesue0317.tistory.com/27
[Data Science] 지도학습과 비지도학습이란 ?
데이터 마이닝이란 대량의 데이터를 탐색하고 분석하여 의미 있는 패턴과 규칙을 발견하는 것입니다. 또한, 예측이 주된 목적입니다. 이러한 데이터 마이닝에는 다양한 기법들이 존재합니다.
piscesue0317.tistory.com
지도학습이란 y = f(x) 에 대해
입력변수 (X) 와 출력변수 (Y)의 관계에 대하여 모델링하는 것입니다.
즉, Y에 대해 예측하거나 분류하는 문제를 다룹니다.
https://piscesue0317.tistory.com/34
[Machine Learning] 선형 회귀분석 ( 지도학습 / 예측 )
https://piscesue0317.tistory.com/27 [Data Science] 지도학습과 비지도학습이란 ? 데이터 마이닝이란 대량의 데이터를 탐색하고 분석하여 의미 있는 패턴과 규칙을 발견하는 것입니다. 또한, 예측이 주된 목
piscesue0317.tistory.com
먼저, 간단히 선형회귀분석에 대해
알아보도록 하겠습니다.
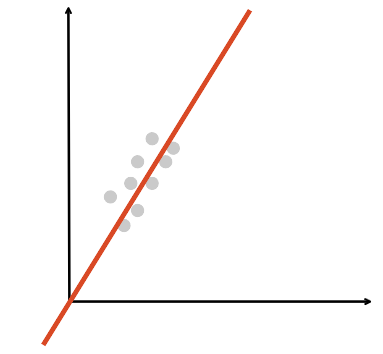
선형회귀분석은 위 그림처럼
연속형 종속변수와 독립변수 간 직선 관계를 가정하고,
이들 간의 수학적 관계를 밝힙니다.

만약 이러한 형태면 어떻게 될까요 ?
선형 회귀분석에서 처럼
직선 관계를 가정할 수 있을까요 ?
그렇지 않습니다.
위 글에서도 다뤘다시피
선형 회귀분석은 종속변수가 범주형인 경우는
사용이 불가합니다.
즉, 분류 문제에는 사용할 수 없는
알고리즘이라는 뜻입니다.
그러면 어떠한 방식으로 해결할 수 있을까요 ?
이 질문에 대한 해답이 바로
이 글에서 다룰 '로지스틱 회귀분석' 이라는
알고리즘입니다.
선형 회귀분석과 이름이 비슷한데,
어떠한 차이점 때문에 분류 문제를 해결할 수 있는지
알아보도록 하겠습니다.
로지스틱 회귀분석 이란 ?

결론적으로 선형 회귀모형이
범주형이라는 종속변수의 특성을 고려해야 하는 것이 핵심입니다.

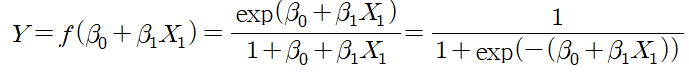
이때, 로짓 함수를 통해
선형 회귀모형을 S자형 회귀모형으로 변형시켜
범주형 종속변수도 고려하게 됩니다.
* 로짓 함수 : S자 모형으로 증가하거나 감소하는 함수


위 식의 양변에 log를 취함으로써
로지스틱 회귀모형을 선형관계로도 만들 수 있습니다.

로지스틱 회귀분석은 이처럼
예측확률이 독립변수의 값의 증감에 따라 함께 증감하고
0과 1 사이의 값을 갖는 확률값으로 변환하여 비선형성을 나타내는 기법입니다.

즉, 어떤 사건이 발생할지에 대한 예측이 아니라
그 사건이 발생할 확률을 예측합니다.
예를 들어, 독립변수 (X) 인 소득을 사용하여
개인 대출 여부 (Y) 를 예측하고자 합니다.
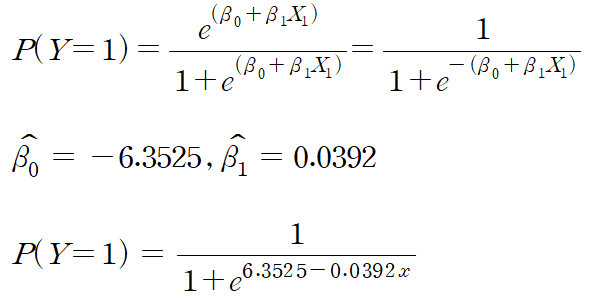
이때 위와 같은 식이 도출되었을 때,
소득이 200인 사람의 개인 대출 여부는 0.82가 됩니다.

* 로지스틱 회귀모형에서의 회귀계수는
최대우도법을 활용해 추정합니다.
단일 독립변수

로지스틱 회귀분석도 단순 선형 회귀분석과 유사하게
단일 독립변수 X와 종속변수 Y의 관계를 직선으로
표현할 수 있습니다.
다중 독립변수

또한, 다중 선형 회귀분석처럼
다중 독립변수 X와 종속변수 Y의 관계를 직선으로
표현할 수 있습니다.
승산

로지스틱 회귀분석에서는 승산 (Odds) 이라는 개념이 등장합니다.
승산은 집단 1 (성공) 에 속할 확률과 집단 0 (실패) 에 속할 확률 간의 비율을 의미하며
이를 성공확률 / 실패확률 으로 나타냅니다.
즉, 집단 1에 속할 확률이 집단 0에 속할 확률의
몇 배인지를 알 수 있습니다.
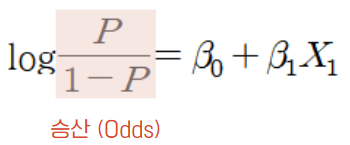
또한, 위 식을 활용하면
로짓은 log(승산) 이라고 할 수 있습니다.
따라서 로지스틱 회귀분석은
로짓을 종속변수로 정의하고 로짓과 q개의 독립변수와의 관계를
선형함수로 모형화한 것입니다.
그렇다면 승산이라는 개념이 왜 등장한걸까요 ?

선형 회귀분석에서는 x1이 증가하면
y가 0.3067만큼 증가함을 알 수 있습니다.

반면, 로지스틱 회귀분석에서 x1이 증가하면
y는 얼마큼 변화할까요 ?
이때 앞서 배운 승산이라는 개념이
활용됩니다.

이를 통해 선형 회귀분석에서처럼
x값이 변화할 때의 y값의 변화량을 알아낼 수 있습니다.
결론적으로 x1이 증가하면
e^0.625 만큼 y가 증가하게 됩니다.
승산비

승산비 (Odds ratio) 는
앞서 배운 승산의 비율로 나타냄으로써
독립변수의 종류에 따라 다양한 해석을 해냅니다.

수치형 독립변수의 경우,
특정 독립변수가 분류 결정에 미치는 영향 정도를 표현합니다.

범주형 독립변수의 경우,
두 범주를 비교하기 위해 사용됩니다.
예를 들어, 전문직 교육 유무를 나타내는 범주형 독립변수 (x) 의 승산비를 이용하여
전문직 교육을 받은 고객과 전문직 교육을 받지 않은 고객에 대한
대출 승인 (y) 의 승산을 비교할 수 있습니다.

결론적으로 위 식들이
모두 로지스틱 회귀모형입니다.
'ML > Algorithms' 카테고리의 다른 글
| [Machine Learning] 군집분석 (비지도학습 / 데이터 축소) (0) | 2023.02.13 |
|---|---|
| [Machine Learning] SVM (지도학습 / 분류) (0) | 2023.01.28 |
| [Machine Learning] KNN (지도학습 / 예측 & 분류) (0) | 2023.01.12 |
| [Machine Learning] 의사결정나무 (지도학습 / 분류) (0) | 2023.01.12 |
| [Machine Learning] 의사결정나무 (지도학습 / 예측) (0) | 2023.01.12 |




