| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- dataframe
- 시계열 데이터
- 지도학습
- ML
- 단순선형회귀분석
- 잔차분석
- scikitlearn
- Python
- 선형회귀분석
- 데이터전처리
- machinelearning
- DataScience
- 의사결정나무
- 손실함수
- LogisticRegression
- 비지도학습
- 분류
- RegressionTree
- 데이터분석
- GridSearchCV
- 하이퍼파라미터
- 로지스틱회귀분석
- 결정계수
- deeplearning
- LinearRegression
- 다중선형회귀분석
- time series
- 시계열데이터
- OrdinalEncoder
- 딥러닝
- Today
- Total
IE가 어른이 되기까지
[Machine Learning] SVM (지도학습 / 분류) 본문

이번 글에선
Support Vetor Machine (SVM) 이라는
알고리즘에 대해 다뤄보고자 합니다.
SVM도 KNN, 로지스틱 회귀분석, 분류나무 등처럼
분류 알고리즘에 속합니다.
SVM은 종속 변수 형태에 따라
범주형 변수는 Support vector classifier,
연속형 변수는 Support vector regression 으로 나뉩니다.
이 글에서는 Support Vector Classifier에서만
다루도록 하겠습니다 !
SVM 이란 ?

위와 같은 그림에서
우리는 빨간색, 파란색 점을 분류할 수 있는
다양한 선형 분류 함수가 존재합니다.

SVM은 빨간색, 파란색 집단 사이의 간격,
즉 마진이 최대가 되도록 하는 최적의 선형 분류 함수를 탐색합니다.
이때 선형함수에 맞닿아 있는 관측치들을
Support Vector이라고 합니다.
최적의 선형 분류 함수 탐색하기 = 최대 마진
그렇다면 마진이 최대가 되도록하는
최적의 선형 분류 함수는 어떻게 탐색하는 것일까요 ?
먼저, 점과 직선 사이의 거리 계산에 대해
알아보도록 하겠습니다.


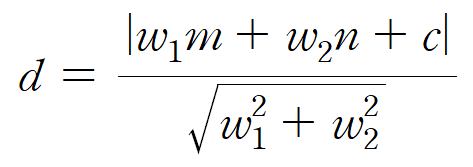
따라서 한 점과 직선 간의 거리는
위와 같은 공식으로 나타낼 수 있습니다.
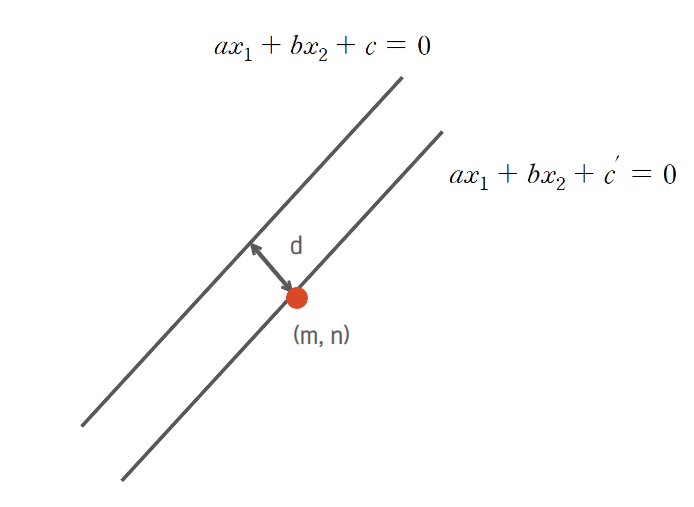
이를 활용하여 우리가 구하고자 하는
두 직선 간의 거리인 마진을 구할 수 있습니다.
만약 (m, n)이

위의 한 점이라고 가정하면, 두 직선간의 거리는
한 점과 직선간의 거리와 동일해집니다.




또한, 위 과정을 행렬 형태로 변환하여
최대 마진을 구할 수도 있습니다.


결국 SVM에서는 마진인 d를 최대화하는 것이
목적이 되겠죠 ?
분리가능한 선형 SVM 학습
SVM은 최적화 문제라고 할 수 있습니다.

최적화는 어떠한 목적함수를 최소화시키는 방법론을 말하는데,
우리가 최대화시키고자 했던 마진의 분모와 분자를 바꾸면
최적화 이론과 같아지게 됩니다.
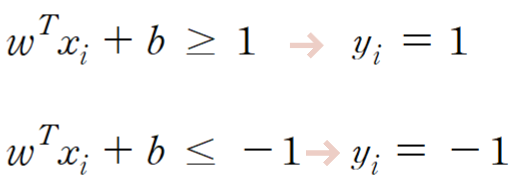
이므로

입니다.
위는 Primal 문제입니다.

KKT condition에 의해서
Primal 문제를 Dual 문제로 변환하면 위와 같아집니다.
Dual은 관측치 간의 유사도를 통해
각 클래스를 지정해 줍니다.

위와 같은 방식을 통해
신규 관측치가 들어오더라도 클래스를
분류해 낼 수 있습니다.
분리불가한 선형 SVM 학습

하지만 만약 데이터가 위와 같이 분포해 있다면
선형 분류 함수로 분리해 낼 수 있을까요 ?
불가능합니다.
이를 해결하기 위해
크사이라는 용어가 등장합니다.

크사이는 위 그림에서 볼 수 있다시피
분리 불가한 선형 SVM을 학습하기 위해 해당 클래스의 직선과의
거리를 나타내는 것입니다.
분리불가능한 선형 SVM은
SVM의 최적화 Primal 문제를 변형하여 학습을 진행합니다.

이때, C는 크사이를 최소화하는 것에 비중을 둘 것인지,
마진을 최대화하는 것에 비중을 둘 것인지를 결정하는 상후이며
이는 분석자 혹은 실험을 통해 결정합니다.
Ex)
C = 10 : 오류 최소화에 비중
C = 1 : 비중 동일
C = 1/10 : 마진 최대화에 비중


분리 불가능한 선형 SVM 학습 또한
KKT condition을 통해 Primal 문제를 Dual 문제로 변환하면
위와 같아집니다.
비선형 SVM

만약 이처럼 선형 분리조차 안 되는
데이터는 어떻게 하면 될까요 ?
두 가지 방법이 존재합니다.

1.
모든 관측치들을
선형 분리 가능하도록 매핑 함수를 이용하여
차원을 증가시킵니다.

이처럼 개별 관측치를 매핑함수를 통해
고차원 관측치로 만들어 이들의 내적을 목적함수에 넣습니다.
2.
만약, 고차원의 내적값을 바로 구할 수 있다면
매핑 함수 없이 Kernel 함수를 사용해 바로 고차원의 내적값을
계산할 수 있습니다.

이를 Kernel Trick 이라고 합니다.
* Kernel Trick : 매핑함수로 모든 관측치들을 고차원으로 변환하지 않고,
고차원의 유사도를 Kernel 함수를 이용하여 계산하는 방식
SVM 특징
장점
- 일반화 성능이 우수함, 즉 과적합 되는 경우가 적음
- 오류 데이터 영향을 적게 받음
- 최적화 방법에 의해서 최적의 모델 도출
- Kernel trick을 통해서 고차원의 데이터로 확장 가능
단점
- 데이터가 많아지게 되면 계산 시간이 많이 걸림
- 최적화해야 하는 하이퍼파라미터가 다수
- 해석이 어려움
'ML > Algorithms' 카테고리의 다른 글
| [Machine Learning] 주성분 분석 (비지도학습 / 데이터 축소) (0) | 2023.02.14 |
|---|---|
| [Machine Learning] 군집분석 (비지도학습 / 데이터 축소) (0) | 2023.02.13 |
| [Machine Learning] 로지스틱 회귀분석 (지도학습 / 분류) (0) | 2023.01.17 |
| [Machine Learning] KNN (지도학습 / 예측 & 분류) (0) | 2023.01.12 |
| [Machine Learning] 의사결정나무 (지도학습 / 분류) (0) | 2023.01.12 |




